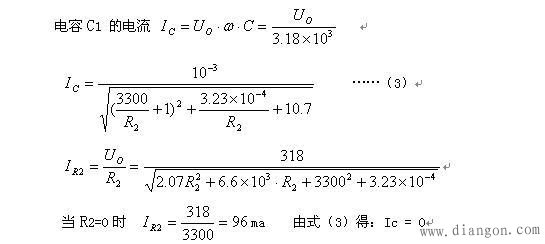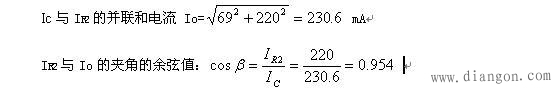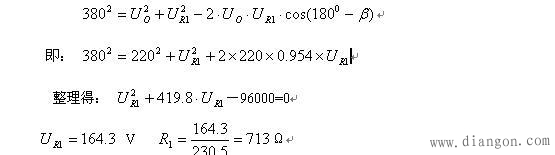交流电路的阻容降压计算公式分析
|
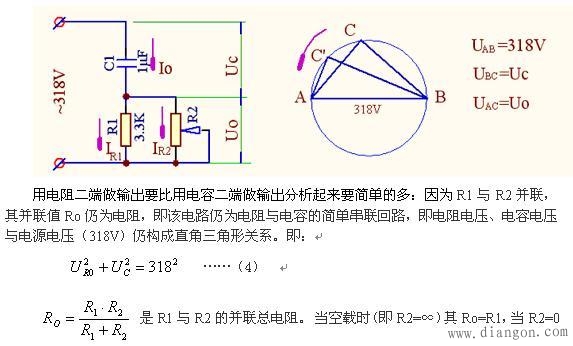
一个1微法电容其最大容许流过的电流=70ma。如将其接在220V交流电源上可行否?如果将该电容接在另一交流电源上,其电容电流=100ma,即超过电容最大容许流过的电流,如用阻容降压的方法降压,应串接多大阻值的电阻使其电容电流=70ma? 串接电阻后,如用电容二端做输出,其空载下输出电压=?如用电阻做负载并接电容二端,当负载电阻由大变小时,其输出电压是否变化?如变化其输出电压是增大还是较小?电容的电流又是如何变化。 串接电阻后,如用电阻二端做输出,其空载下输出电压=?如用电阻做负载并接电阻二端,当负载电阻变小时,其输出电压是否变化?输出电压是增大还是较小?电容的电流又是如何变化。 我的分析:电容通常提供的参数主要是耐压与电容值,在规定的耐压范围内,使用电容,一般都不会击穿。在交流电路中,电容的容抗 Zc= 1/ωC, ω为角频率(ω = 2πf),如f = 50Hz,则ω=314。如电容二端施加一电压U,则电容的电流 Ic=U*ωC。施加最大耐压Um 时的电容电流,就是该电容容许的最大流过的电流。如果施加的电压超过规定的耐压值,虽然电容的电流可以增大,但电容极易被击穿。下面分几个问题进行分析: 1、电容的电压 Uc=I /ωC,如流过1微法电容的电流为70mA=0.07A,电流频率f=50Hz,则:电容的电压Uc=0.07÷(314×0.000001)= 223 V,如果70mA是1μF电容的最大容许电流,则该电容的耐压=223V,即可以将1μF电容直接接在220V交流电源上,不过此时是该电容工作在其耐压的上限值区,若长时间工作不太可靠的,一般选择电容的耐压参数应大于工作电压的2~3倍。 2、 如果该电容直接接在另一电源上,使流过电容的电流=100mA,则另一个电源的输出电压应 =0.1÷(314×0.000001)= 318 V,由于该电容耐压=223V,故此电容工作在318V电压下会因过电压而击穿的。 在此情况下,可以通过串接一电阻来降低电容的电压:如电源电压U=318V,1μF电容的电压要保持 Uc=220V(即电容电流=70mA时的电容电压),则串接的电阻电压UR=:
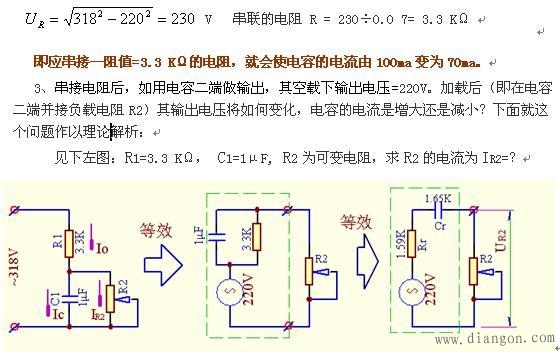
左一图为阻容降压,以电容为输出且带有负载电阻R2的实际电路图,左二图与左图三为左一图按戴维南定理转换成的等效电路图。 左图二中RC为作图一的R C值,其电容容抗 Xc =1000000÷314 = 3.18 KΩ 电阻 R1 = 3.3 KΩ 左图三中的Rr、Xr为由左图二中并联的R C转换为等效的串联R C值,其Rr=1.59 KΩ,Xr=1.65KΩ
IR2 = 220÷3.07 = 71.66 Ma
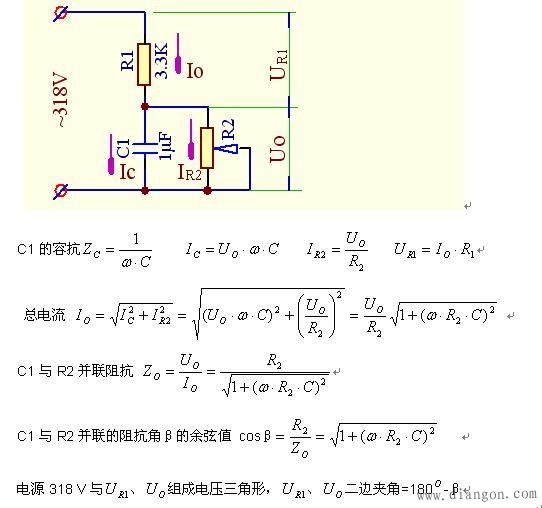
见下图:R1电阻的电压为UR1,电流为Io, C1的电压为Uo, C1的电流为Ic,R2的电压为Uo,R2的电流为IR2,
即:当R2=0时,短路电流就等于电源电压除以R1的电阻值。而此时电容的电流=0 验算: 式(2)与式(3)即为阻容降压且以电容二端做输出的电路,其输出电压Uo、电容电流Ic与负载电阻R2的数学关系式。下面取不同阻值的负载电阻R2进行计算,看其输出电压Uo与电容电流的的变化趋势: 1、空载时:其R2 = ∝,将R2带入式(2),其分母值=2.07,计算的结果:Uo≈220V. 此时电容电流 Ic=220÷3180≈70 ma 2、加载时,如R2=5KΩ,带入式(2),其分母值=3,53,计算的结果: Uo=169V 此时电容电流 Ic=169÷3180=53.1 ma 如R2=1KΩ,带入式(2),其分母值=19.5,计算的结果: Uo=72V 此时电容电流 Ic=72÷3180=22.6 ma 3、短路时:即使R2=0, 带入式(2),其分母值= ∝,计算的结果: Uo=0V 此时电容电流 I c= 0÷3180 = 0 ma 可见:阻容降压,由电容二端做输出,空载时电容中流过的电流最大,输出电压最高。加载后,随着加载变大(即R2变小)电容的电压逐渐降低,其流过电容的电流也随之变小。而负载电阻R2由无穷大(空载)逐渐↓0时,其电流由0变大,当R2=0时,其短路电流=电源电压除以电阻R1。 4、串接电阻后,如用电阻二端做输出,其空载下输出电压=230V。加载后(即在电阻R1二端并接负载电阻 R2)其输出电压将如何变化,电容的电流是增大还是减小?见下图:
时其Ro=0。即:空载时输出Uo等于R1与C1串联电路R1的电压值。 上左图中的ABC三角形即为R1、C1、与电源318V的电压三角形:其AB边为圆的直径,它表示为电源电压(318V)矢量,AC边表示为Uo的电压矢量,BC边表示为Uc的电压矢量。二直角边的交点C点位于以AB为直径的圆上。当并上R2且使R2由=∝逐渐小直至=0时,其并联等效电阻Ro值将由=R1逐渐变小直至=0。在此变化过程中,Uo与Uc和电源318V组成的电压三角形始终为直角三角形,由于斜边AB(即电源318V)保持不变,故不同R2值对应的直角三角形的顶点都位于CA圆弧线上,且由C点移向A点。当R2=0时输出电压Uo=0(即AC边=0),此时电压三角形变为一条直线且与AB边重合,,··顶点C移到左图中的A点处。此时Uc=318V。 即:在R2由无穷大(空载)逐渐↓0时,其对应的直角电压三角形的顶点C将沿AC弧线由C点移向A点。从图中可以看到Uo与Uc的变化趋势。 在R2由无穷大(空载)逐渐↓0时,输出Uo电压由空载时的230V逐渐↓0,而Uc电压由空载时的220V逐渐↑到3118V。在整个变化过程中,电容C1的电流由空载时的70ma逐渐上升到100ma,电阻R1的电流由空载时的70ma逐渐下降到0,而负载电阻R2的电流变化却是:由0逐渐上升到最大值(即R2短路,318V施加C产生的电流)。见以下推导:
即:R2=0时,其短路电流就等于电源电压除以电容的容抗值。 5、如以电容二端做输出,负载固定,要求输出电压=Uo,应串多大电阻的计算: 设电源电压为380V,用阻容串联的方式降压输出(以电容二端作输出),其电容器容值=1μF,与之并联的负载电阻R2=1KΩ,求应串多大电阻?确保输出电压=220V? 解:1、先求出输出电压Uo=220V时,电容C与电阻R2的电流: Ic=Uo·ω·C=220×314×10=69 Ma Ic的相位引前Uo相位90 IR2=Uo / R2 = 220÷1000=220 mA IR2的相位与Uo同相位。
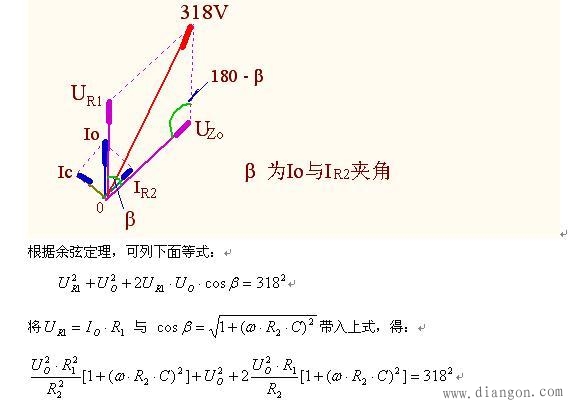
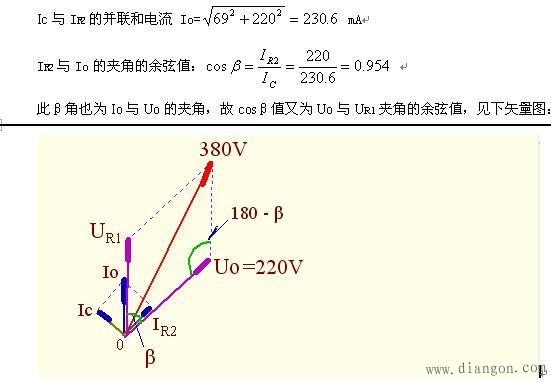
此β角也为Io与Uo的夹角,故cosβ值又为Uo与UR1夹角的余弦值,见下矢量图:
电阻R1的电压UR1=Io·R1, UR1的相位与Io同相位,由上图可知:Uo与UR1的(矢量)和电压=380V,据余弦定理可列下等式:
答:应选阻值为713欧电阻与电容C串联,可确保R2=1KΩ时输出电压Uo=220V 从上述分析、计算可知: 1、电容通常提供的参数主要是耐压与电容值,知道电容的耐压值,就可得知电容的最大容许流过的电流值。反之知道电容的最大电流值,也可得知电容的耐压值。 2、电容在交流电路里,可以通过串接电阻改变电容的电压,其电阻与电容的电压比等于电阻与电容的阻抗比。 3、在电阻与电容串联的电路,无论以电阻或电容二端做输出,其输出电压是不稳定的、是随负载变化而变化的:其输出电压会随着负载电阻减小而变小。当负载电阻=0时,输出短路电流=阻容串联的电路电压U 除以与输出端相串联的元件的阻抗值Zx:如以电容二端为输出口,其短路电流=U / R。如以电阻二端为输出口,其短路电流=U / Zc=U·ω·C. |