在电路的求解过程中, 如果不要求计算全部支路的电压、电流,而只计算某支路的 电压、电流或功率时,应用回路(网孔)电流法和结点电压法列写方程进行求解将十分繁琐,而采用一端口网络定理即戴维南/诺顿定理求解则较简便。
戴维南定理指出:任何线性含源一端口网络对于外部性能来说,可以用一个电压源等效代替。其电压源的电压等于原一端口网络的开路电压Uoc,其内阻等于原一端口网络变为无源一端口网络后的入端电阻Req。应用戴维南定理的关键是求开路电压和入端电阻。
诺顿定理指出:任何线性含源一端口网络对于外部性能来说,可以用一个电流源等效代替。电流源的电流等于原一端口网络的短路电流Isc,其内电导Geq(或电阻Req)等于原一端口网络变为无源一端口网络后的入端电导Geq(或电阻Req)。应用诺顿定理的关键是求短路电流Isc和入端电导Geq。 |
|
1、戴维南定理
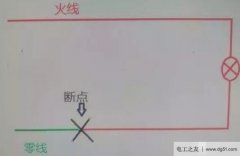
图1.14(a)中,电路结构和参数已给定,应用戴维南定理求电流I=?(图中电阻的单位为欧姆)。
分析:应用戴维南定理的关键是求出a,b两端的开路电压Uoc和入端电阻Req。Uoc等于ab两端将负载开路后的电压;Req等于将ab左边的含源二端网络变为无源二端网络时的入端电阻。 求开路电压的等效电路如图(b)所示,方法不限。本题用结点电压法。入端电阻的等效电路如(c)所示;利用图(d)求出待求量。
方程式及结果如下:
将负载开路,如(b)。在(b)中求ab两端的开路电压Uoc:
[(1/R1) (1/R2)]Uoc=(Us1/R1) IS 代入数据, 解得 Uoc=32V
为求入端电阻,在(b)中,将独立源置零,如(c)。则ab两端的入端电阻: Req=4 5//20=8Ω
则戴维南等效电路如图(d)。电流 I=32/(8 2)=3.2A |
 |
|
2、诺顿定理
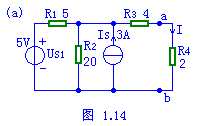
图1.15(a)中,电路结构和参数已给定,用诺顿定理求电流I=?(图中电阻的单位为欧姆)。
分析:应用诺顿定理的关键是求出a,b两端的短路电流Isc和入端电阻Req(或电导Geq),Isc等于ab两端将负载短路时的电流如图(b)所示;Req(或电导Geq)等于将ab左边的含源二端网络变为无源二端网络时的入端电阻(或电导), 其等效电路如 (c)所示;最后利用图(d)求得待求量。
方程式及结果如下: |
 |
将负载短路如(b)。在(b)中求短路电流Isc,采用结点电压法:
Unc=[(25/5) 3]/[(1/5) (1/20) (1/4)]=16V
代入数据,解得Isc=16/4=4A
为求入端电阻,在(b)中,将独立源置零,如(c)。则ab两端的入端电阻: Req=4 5//20=8Ω
则诺顿等效电路如图(d)。电流 I=4*[8/(8 2)]=3.2A
|
|
3、含有受控源的戴维南定理
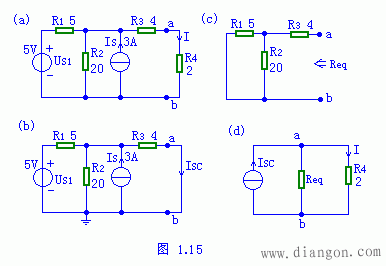
图1.16(a)中,电路结构和参数已给定,求:电流I=?(电阻的单位为欧姆)。
分析:该电路中含有CCCS,为了求开路电压Uoc,仍须将ab支路断开如图(b)所示,用任意方法求开路电压,根据电路特点用结点电压法。当电路中有受控源时求入端电阻的方法与无受控源时不太一样。有两种方法可采用,一是除独立源后,加压求电流,入端电阻Req=u/i,如(c)所示,可用任意方法求出u/i,本题采用基尔霍夫定律。最后利用图(d)求出待求量。
方程式及结果如下: |
 |
将负载开路,如(b)。在(b)中用结点电压法求开路电压Uoc,方程如下:
[(1/7) (1/15)]Un=2I0 (8/7)
(5 10)I0=Un 代入数据,解得 UOC=(10/15)Un=10V
为求入端电阻,在(b)中,将独立源置零,在a,b间加电压u,如(c)。方程如下:
U=10I0
U=5(i-I0) 7(i-I0 2I0) 代入数据,联立解得 Req=U/i=8Ω
则戴维南等效电路如图(d)。 I=(Uoc-US2)/(Req R4)]=0.5A |
|
4、戴维南定理综合题目 图1.17(a)中,参数已给定,求R中的电流I=?
分析:该电路中含有CCCS,解题思路与上一题类似,为了求开路电压Uoc仍须将ab支路断开如图(b)所示,用任意方法求开路电压。本题用网孔电流法,网孔电流如(b)红线所示。在含有受控源的电路中,求入端电阻除了采用除独立源加压求电流外,还可以用开路电压除以短路电流,即Req=Uoc/ISC求入端电阻。首先将负载短路,如(c),其中短路电流ISC,可用任意方法求短路电流ISC。最后得到戴维南等效电路(d),即可求I。
方程式及结果如下: |
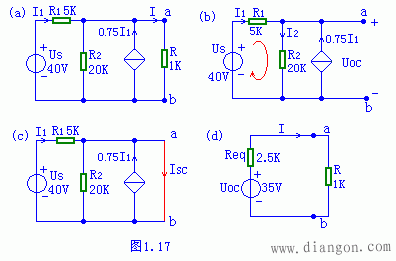 |
将负载开路,如(b)。求开路电压Uoc可直接利用KCL:I2=I1 0.75I1=1.75I1
在左边的网孔中:5000I1 20000I2=40 代入数据,解得 UOC=20000I2=35V
在(c)中将负载短路,求短路电流ISC:I1=40/5k=8mA 则ISC=I1 0.75I1=14mA
Req=UOC/ISC=2.5KΩ
图(d)中 I=35/(2.5 1)*1000=10mA
|
|
5、最大功率传输定理
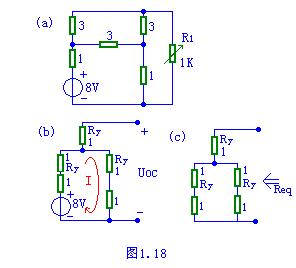
图1.18(a)电路中,求R为何值时,负载 R 可获得最大功率,并求出Pmax。(图中未标电阻的单位为欧姆)。
分析:根据最大功率的传输定理,当负载电阻等于电压源的内阻时,负载可获得最大有功功率。因此本题的关键是求出该电路的戴维南等效电路。即Uoc如图(b)和Req如图(c)所示。具体计算过程和以上题目类似,计算过程中用到电阻的三角形与星形之间的转换。
方程式及结果如下: |
 |
|
首先将三个3Ω电阻等效转换成Y型连接RY=1Ω, 网孔电流 I=8/4=2A
则:Uoc=2I=4V
在(c)中求ab两端的入端电阻:Req=1 2//2=2欧,
因此根据最大功率传输定理:当R=2Ω时R可获得最大有功功率
Pmax=( Uoc*Uoc)/4*Req=2w | |