用电子秤测步进电机矩角特性
时间:2023-03-20来源:佚名
|
1 引 言
永磁步进电动机通常要求测矩角特性。所谓矩角特性,即在一个步距角范围内,静力矩与角位移之间的关系。一般矩角特性的关系曲线如图1所示。
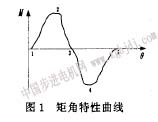 图1中θ为一个步距角。θ/2即曲线3处,静力矩,即曲线2.4处,静力矩最大。曲线1、2处和5、4处,为静力矩上升段;曲线2、3和4、3处,为静力矩下降段。可以看出,测量矩角特性并不简单,它不能用简单吊砝码方法进行测量。因吊砝码只能测试曲线的上升段,即图1曲线中的1-2段和5-4段(5-4段用反向吊砝码测试),此2处角位移增大,静力矩增大。但是,进入曲线下降段,即图1曲线中的2-3段和4-3段,此2处角位移增大,静力矩反而减小,吊砝码则无法找到平衡点,测试无法进行。为了测试静力矩的下降段,因必须将步进电机夹在力矩仪上进行。然而,这样角位移指示又很不方便,不像将电机夹在刻度盘上吊砝码测试简捷。
能否驭其二者和优点,找到一种两全其美的方法测试矩角特性,本文介绍的方法,则是为解决这一问题而设计的。
2测试原理
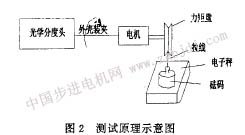
测试示意图如图2所示,它将电机外壳装夹在光学分度头上,电机轴上带一力矩盘,用拉线吊一超重砝码,压在电子秤台面上,电子秤显示出砝码的自重。所谓超重砝码,目的是要使选择的砝码重量,大于电机静力矩最大点拉线拉力的3倍。例如,若电机静力矩最大点拉线拉力为0. lkg,砝码重量则应选择标称值0. 3kg。这样选择的目的,是为了测试时,固定电机转轴不动,摇动光学分度头,只电机机壳转动,二者之间的角位移,便可准确地从光学分度头上读出来。与此同时,二者角位移产生时,静力矩产生,由于静力矩方向与砝码重力方向相反,静力矩的大小便可方便地从电子秤上砝码减轻的重量上自动显示出来,即实现自动平衡测试。静力矩上升段,砝码自动变轻;静力矩下降段,砝码又自动变重,直到静力矩等于零,砝码恢复原重。这样,便克服了单独吊砝码静力矩超过最大点无法平衡的问题。例如,静力矩上升段某点拉线拉力为0. 05kg,砝码自重0.2kg,电子秤上显示砝码读数则为0. 15kg。静力矩下降段,因砝玛重力与拉线拉力自动平衡,各点的静力矩,仍然同上升段一样,从电子秤上减轻的砝码重量上显示出来。角位移为O点,静力矩为O,电子秤则显示砝码的自重0. 2kg。
 3测试实例
以步距角为909的永磁步进电机矩角特性测试为例,测试电压5v,最大静力矩0.013 6Nm,力矩盘半径2cm,选择砝码自重0.2kg。表1是一个步距内00~450的矩角特性和各点测试数据。450~900因需反向吊砝码测试,且测试方法同正向一样,故未列出。
 表1中各点静力矩为拉线拉力乘力矩盘半径2cm。拉线拉力等于砝码自重0.2kg减去电子秤读数。由表1数据可画出该电机的矩角特性,如图3所示
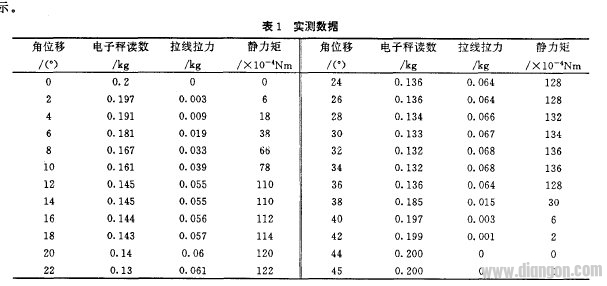 可知,用该法测量静力矩的下降段、准确、可靠。
4应注意的问题
(1) 00位置的确定。该法在拉线无拉力酌情况下,摇动光学分度头,转轴同机壳是一起旋转的。因此,在确定O。位置时,应观察电子秤上砝码自重的变化情况。00位置,光学分度头稍一摇动,电子秤上砝码会自重变轻I退回,砝码恢复自重,读出此点光学分度头上的度数,记为角位移的00。此后便可从O。开始加大角位移,进行各点测试。
(2)砝码重量的选择。砝码自重的选择,建议选择大于拉线拉力的3倍。这是因为,砝码越重,在拉力作用下位移越小。如果砝码自重稍大于拉线拉力,在静力矩最大点处,则会出现混乱,电子秤读数不准确。如笔者在进行上述电机测试时,静力矩最大点拉线拉力为0. 068kg,开始选择自重0.lkg砝码测试,则出现上述混乱现象,后选择自重0. 2kg砝码,才得到满意结果。
5结语
优点从上面叙述中已经知道,缺点是该法光学分度头输出轴上要承受力矩,这对精密的分度装置不利。不过,静力矩小于0. 02Nm,不会对分度头产生多大影响,静力矩大于0. 02Nm的电机,则不宜用上法测试。为了解决这一问题,也可采用同样的电子秤方法,将电机夹在刻度盘上进行,机壳上带一指针,转动机壳,便可在刻度盘上指示角位移。只是角位移指示准确度比光学分度头差。但角位移准确度不一定要求很商,它只须观察静力矩在整个角位移范围内的变化即可。由此可见,当静力矩较大时,也可降低电压,减小静力矩,仍可夹在光学分度头上进行测试。 |