利用六西格玛技术改进发动机冷却风扇设计

利用六西格玛设计技术改进发动机冷却风扇的设计，一般会遵循流行的定义、测量、分析、改进和控制（DMAIC）六西格玛方法，使用设计工具为matlab、统计工具箱、曲线拟合工具箱和优化工具箱。

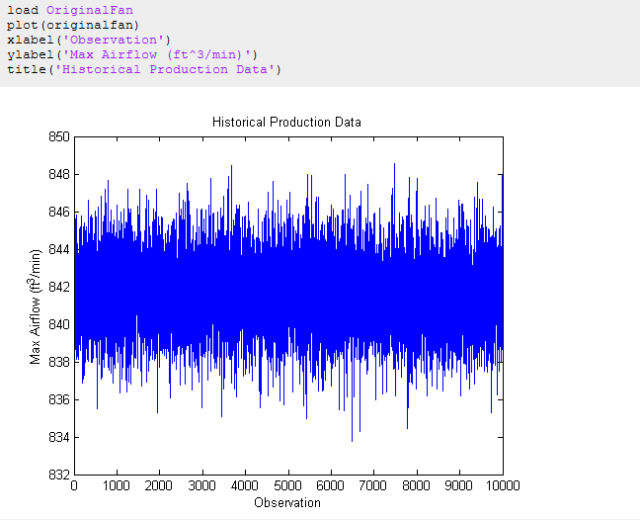
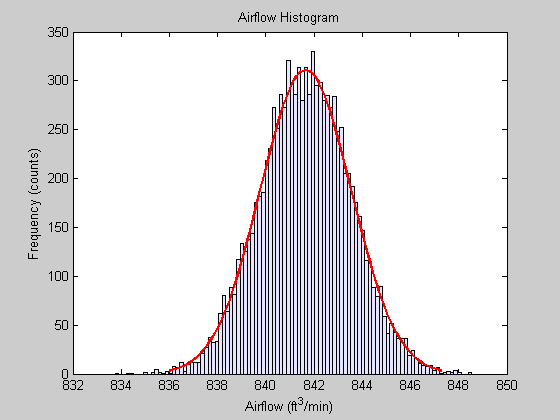
定义问题

我们有一个发动机冷却风扇设计，它无法通过散热器吸入足够的气流，从而在困难的条件下（交通堵塞、天气炎热）保持发动机冷却。根据系统级分析，我们估计需要至少875 ft^3/min的气流，以便在困难条件下保持发动机冷却,我们需要评估当前的设计，开发一种替代设计，以实现我们的目标气流。

测量冷却风扇性能

我们有一个10000个现有冷却风扇性能测量（历史生产数据）的数据库，评估数据，了解当前风扇的性能。

上面的图表显示，数据似乎集中在842 ft^3/min左右，并且有4-6 ft^3/min的变化。虽然这个图很有启发性，但它并没有告诉我们很多关于底层数据的信息；具体来说，它是否遵循正态分布，过程是否处于控制之中（高质量数据）?让我们更详细地研究一下数,“OriginalFan”中的数据是每天进行的一系列测量。在50天的时间内测试了200个风扇/天。我们可以使用统计过程控制（SPC）方法检查数据是否有异常，一种常见的技术是使用Xbar和S图表评估数据。

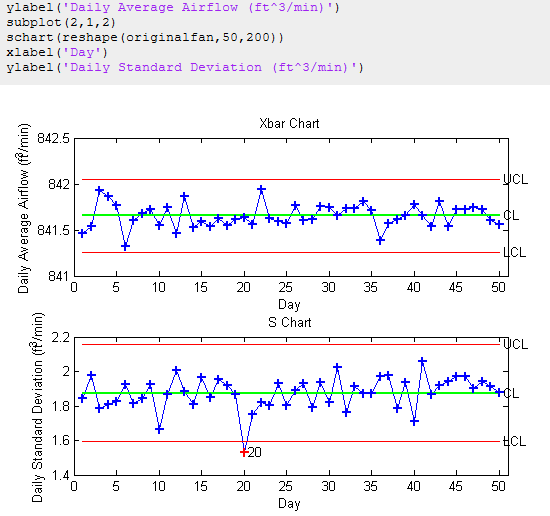
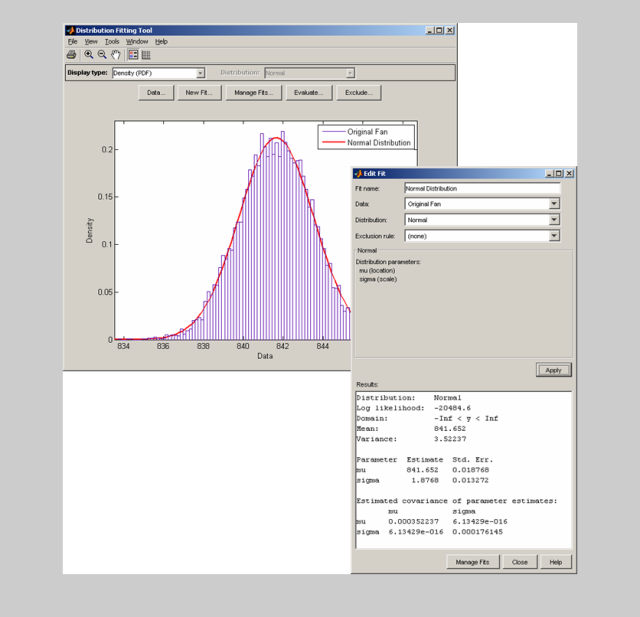
Xbar图表显示了相对于控制限值的日平均值（Cl=平均值，UCL/UCL为 /-3标准偏差）。S图显示了每天的可变性（标准偏差），控制限的定义类似于Xbar图。对于控制图中考虑的过程，每1000个样本中只有3个超出了每个控制范围。只有一天超出了控制范围（第20天，在S图上）。对第20天的数据进行审查后，未发现异常情况，我们得出结论，该过程处于控制状态（异常值被认为是10000次可能发生事件中的3次中的一次）。

在使用Xbar/S图表时，假设数据遵循正态分布，让我们验证一下情况。使用图形工具Dfittool将正态分布拟合到原始风扇数据集。在（数据>选择原始数据，设置bin规则）下将bin值设置为100，创建与数据匹配的分布（新匹配——>匹配名称：正态分布，应用）。注：可以使用“historical_data.dfit”文件加载用于生成下面图片。

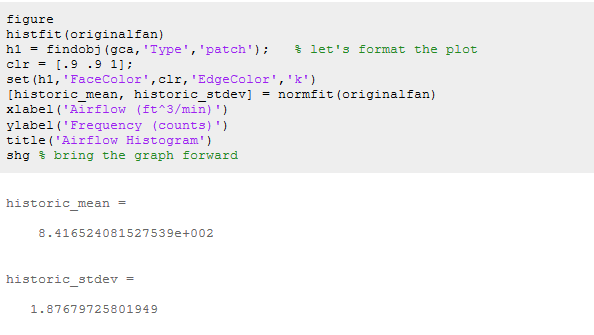
同时，我们可以在与此m文件相同的位置找到它；或者，我们可以在matlab命令行执行与dfittool中相同的操作。

通过看上边的数据的分布，不会接近我们想要的875ft^3/min, 因此，我们需要改进我们的设计。

影响风机性能的因素分析

我们将使用DOE方法来设计并评估冷却风扇,可以修改和控制的因素有：

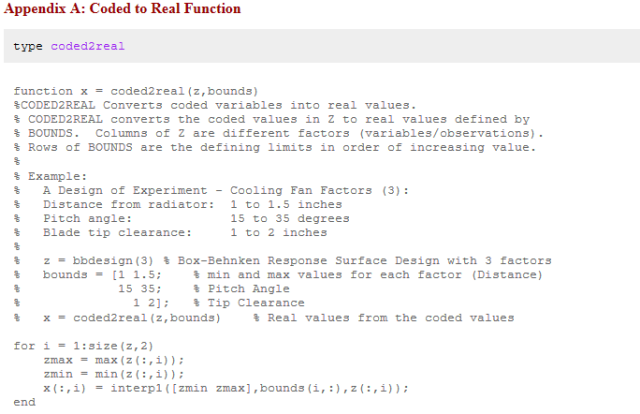
根据以往的经验，我们知道对一个或多个因素会有一个非线性响应，响应为冷却风扇气流速度（ft^3/min），列是因子，行是测试点。因此，我们将使用响应面设计来解释这种非线性，Box-Behnken以编码（规范化）变量[-1，0， 1]来设计生成实验运行。

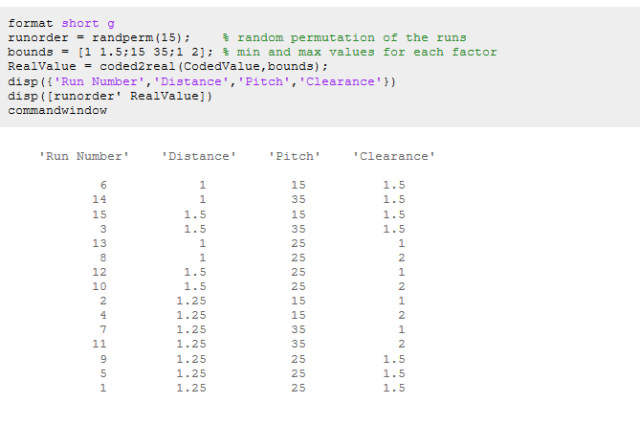
下图为按指定的顺序执行实验，随机化运行顺序，以实际单位显示。

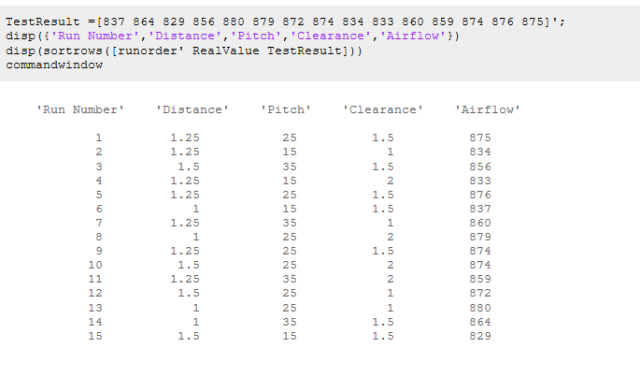
实验得到了以下结果：

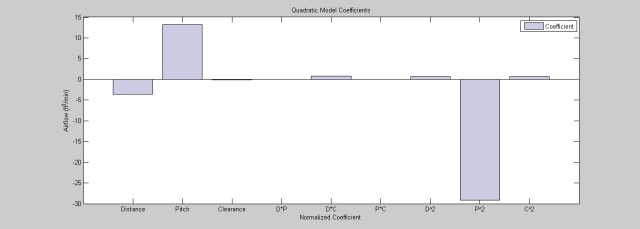
从实验测试结果中，我们发现气流速度对我们改变的因素非常敏感，我们还注意到，上面有四次实验数据达到或超过我们的目标气流速度875 ft^3/min（运行1、4、7和13）。然而，我们不知道这些运行中哪一个（如果有的话）是最佳的。此外，我们不知道对各种因素的变化设计有多强大。我们将根据迄今为止的实验数据创建一个模型，并使用该模型来估计最佳设置下气流对预期因素变化的敏感性。

提高冷却风扇性能

Box-Behnken设计允许我们测试非线性（二次）效应。我们的二次模型的形式是：

我们可以使用regstats来估计和比较系数，并在条形图中直观地显示系数的大小（对于规范化值）。

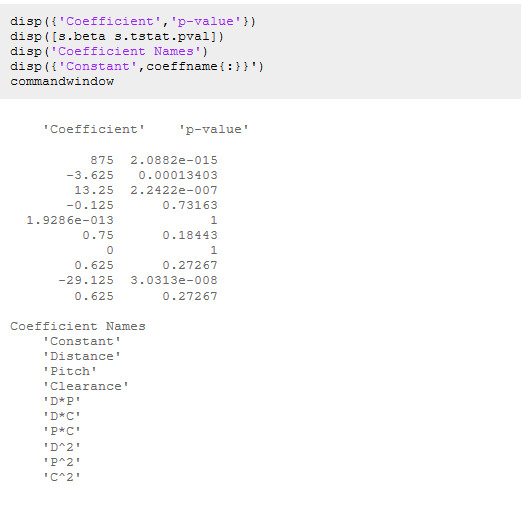
从柱状图中我们可以看出，(Pithch*Pitch)^2是主导因素,我们还可以从系数的条形图中确定影响的大小和方向。除了系数外，我们还可以得到与系数相关的p值，以确定它们在模型中的重要性。

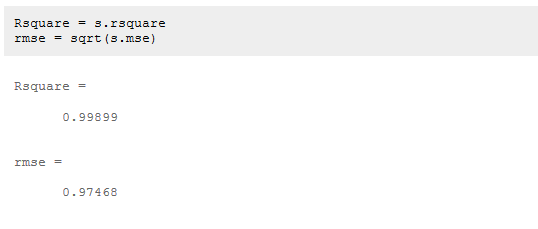
根据p值，常数项、距离、(Pithch*Pitch)^2均具有统计学意义,其中，我们整体模型的平方值和标准差为：

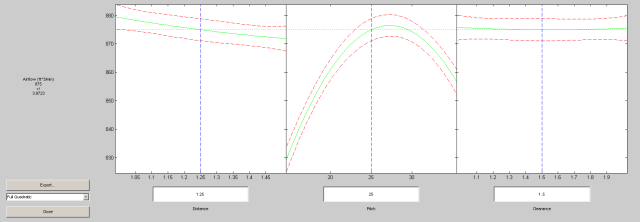
使用rstool可视化我们的模型，可以通过观察响应面来评估模型的适合性，我们可以估计最佳设定点。

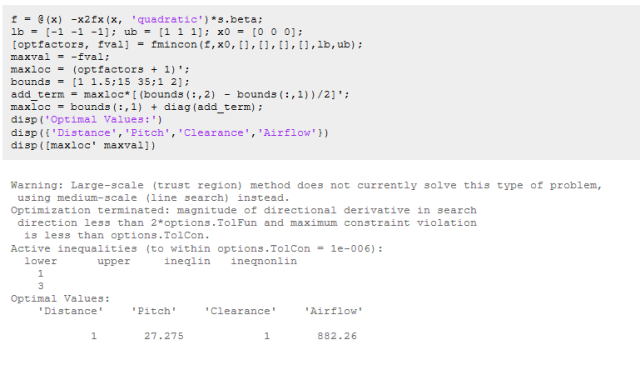
从响应面图可以清楚地看到气流与螺距的非线性关系，虽然可以使用rstool以交互方式确定最佳因素设置，但优化工具箱可以自动执行任务。我们使用带编码值的约束优化函数fmincon（简化边界条件的定义）找到最优因子设置。

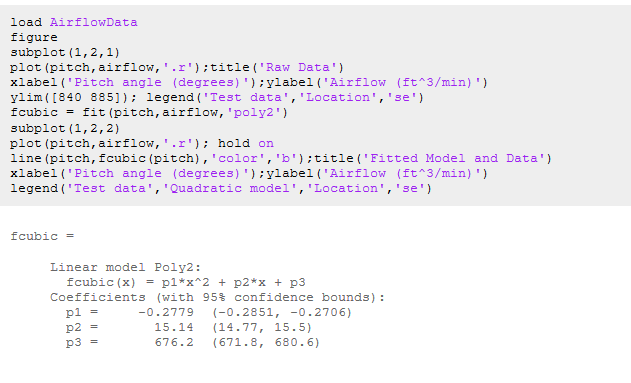
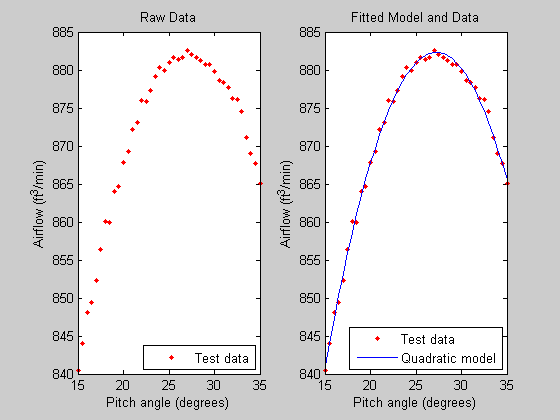
新风扇将放置在距散热器1ft的位置，风扇叶片尖端和护罩之间的间隙为1ft,因为俯仰角对气流有比较大的影响。我们将进行一些额外的测试，验证出27.3°的俯仰角是最佳的，其中，测试中使用可变螺距测试风扇进行的，如下图所示，我们的模型输出的数据，结果表明，采用二次型节距模型是可行的。

目前，我们改进的冷却风扇设计，满足我们的气流要求，我们也有一个模型，根据我们可以在设计中修改的因素，很好地近似风扇性能。在我们可以放心解决问题之前，需要确保风扇性能对制造和安装中的可变性具有鲁棒性，我们根据历史经验将制造不确定性定义为。

我们需要验证这些因素的变化，并将使能够在目标气流周围保持稳健的设计，由于坚持六西格玛的理念，我们还需要实现每1000000个风扇的缺陷率不超过3.4。也就是说，我们需要在达到目标为875 ft^3/min的合格率为99.999%。我们将使用Monte Carlo仿真来验证我们的设计，生成具有10000个样本指定公差的三个因子的随机数，还将包括与模型中的噪声成比例的噪声变量（即拟合模型的均方根误差）。注：我们的模型系数定义为变量分别为：距离、间距和间隙。

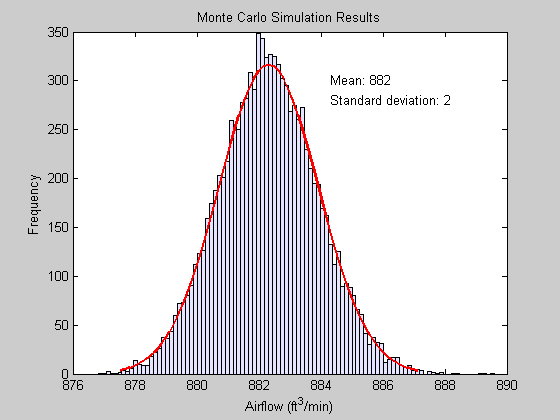
我们的结果看起来很有希望,我们已经获得了882 ft^3/min的平均气流，并且在大多数数据中似乎优于875 ft^3/min，我们来确定875 ft^3/min或更低的概率。

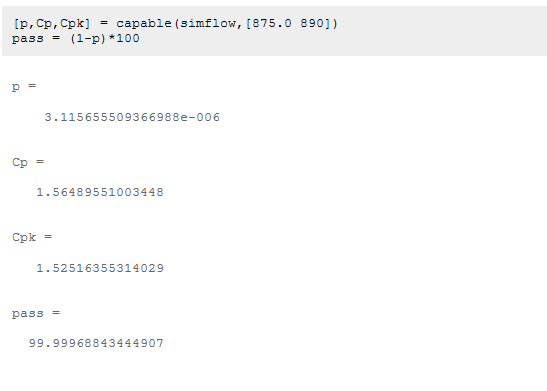
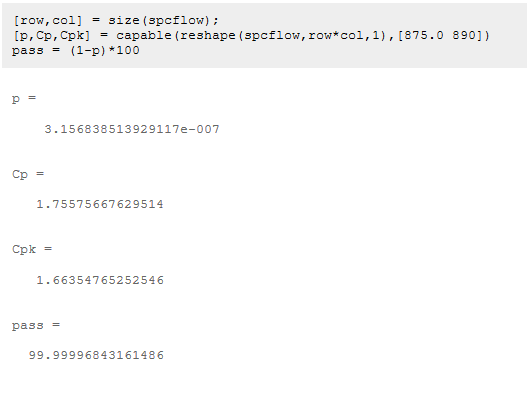
我们的设计似乎能够在99.999%的时间内实现至少875 ft^3/min的气流，可以使用模拟及制造过程中的预期差异来估计过程能力。首先，定义流程的上限和下限，下限已定义为875 ft^3/min，上限将根据电动驱动电机的预期可靠性定义，如果我们通过散热器吸入超过890 ft^3/min的空气，电机的寿命将受到限制，我们将设置890 ft^3/min作为上限，并估计相应的制造能力。

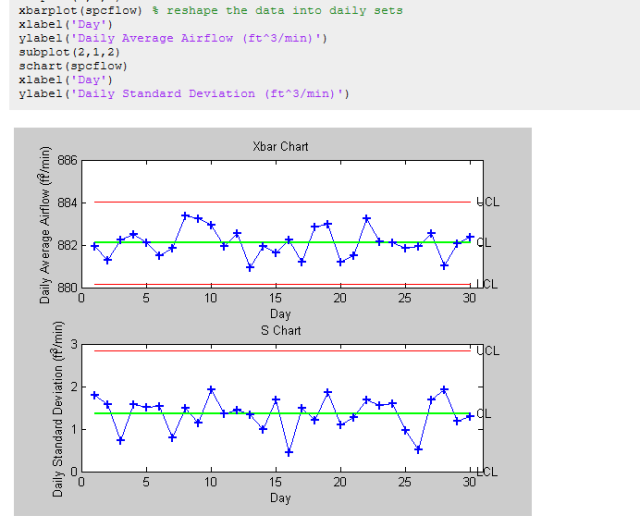
其中，cp值为1.6（>=1.6被视为高质量过程）。CPK表明我们的过程相对于过程极限定义是居中的（CPK〉=CP）。现在，我们需要实施这个设计并监视它，以验证我们的设计过程并确保冷却风扇提供高质量的性能。

控制改进冷却风扇的制造我们使用统计过程控制（SPC）监控和评估制造和安装过程，以确保我们的设计在实践中有效， 最初每天生产五个冷却风扇，评估新冷却风扇生产的周期为30天。

根据结果，我们的制造过程处于统计控制状态，随着时间的推移没有超出控制线或出现非随机模式， 我们还可以对数据进行功能分析，以评估我们的流程。

其中，Cp值1.8大于我们初始评估的1.6，表明该过程的运行变化低于我们的预测， Cpk值为1.6表示我们的过程不在我们定义的上限和下限之内。 我们只会关注低于1.33的Cpk值，此时该过程将高度偏向上限或下限，并且我们更有可能超出我们的规格， 我们的工艺完全在我们的极限范围内，我们在99.999％的时间内达到目标气流（875ft^3/min）。

总结

我们使用六西格玛DMAIC方法与MATLAB及统计工具箱和优化工具箱展示稳健设计的概念， 评估了发动机冷却风扇设计，发现在困难条件下不能通过散热器吸入足够的空气来冷却发动机， 实验设计用于评估对风扇性能影响最大的因素。并根据实验数据开发了一个模型，用于优化风扇设计； 通过跟随测试验证了优化设计，并评估了风扇设计的公差， 由此产生的风扇设计能够达到875ft^3/min或更高的目标，并且合格率达到99.999％。