静电平衡与静电平衡条件
|
静电(píng)衡与静电(píng)衡条件 当带电系统的电荷分布状态稳定不变,从而其电场分布也不随时间变化时,我们称该带电系统达到了静电(píng)衡. 如2.1节所述,导体是体内存在着大量自由电荷或载流子的物体.如果导体内存在电场(不管这电场是导体上的电荷产生的还是外电场),导体内的自由电荷、定会在电场作用下发生移动,从而改变导体上的电荷分布,电荷分布的改变反过来又会影响和改变电场的分布.因此,在有导体存在时,导体上的电荷分布与电场的空间分布将相互影响、相互制约,不是所有的电荷和电场分布都能使导体达到静电(píng)衡的. 现在,我们通过一个具体事例来讨论导体上的电荷分布与电场分布之间的相互影响.把一个原本不带电的导体放入均匀外电场E。中如图2.1(a)所示,由于导体内存在电场E,导体内的自由电荷将沿电场移动,使得在导体右侧出现正电荷,左侧出现负电荷如图2.1(b)所示.导体上出现电荷后,这些电荷产生电场E,E’与E。的方向相反,只要E"不能完全抵消E。,则在电场E=E十E"的作用下,导体内的自由电荷继续移动,使E’增大.当E’大到导体内的电场场强E=E E=0时,导体内自由电荷的移动停止,这时候导体上的电荷分布不再变化,同时电场的空间分布也不再随时间发生变化,导体就达到了静电(píng)衡.导体从放入外电场中处于非静电(píng)衡到达到静电(píng)衡的这个过程,实际上是极迅速的,大约只需10~9 s 的时间.导体达到静电(píng)衡时的电场空间分布情况如图2.1(c)所示.由此可以看出,导体要达到静电(píng)衡,必须满足一定的静电(píng)衡条件. 均匀导体的静电(píng)衡条件是导体内场强处处为零.这里所说的“均匀”导体,指导体的质料均匀,温度均匀. 由静电(píng)衡条件出发,很容易推得有静电(píng)衡导体存在的电场,电场分布必须遵守如下规则: (1)导体是一个等势体,导体表面是一个等势面. (2)靠近导体表面外侧处的电场场强处处与表面相垂直. 这两条电场分布应遵守的规则的证明很简单.因为静电(píng)衡条件要求导体内(包括表面)处处E=0,所以,导体内和表面上任意两点P和Q之间的电势差即导体内和表面上任意两点的电势相等(Up=Ua),所以导体为等势体,表面为等势面.由于场强与等势面相垂直,而导体表面为等势面,故导体外靠近其表面处的场强与表面处处相垂直. 由于导体表面必为等势面,所以有导体时,导体外的场强分布必受导体表面形状的控制与调整,以保证导体表面为等势面.下面将要证明的唯一性定理更表明:若干带电导体产生的电场,完全由这些导体的几体形状、相对位置以及它们的电势或电量所唯一确定.因此可以说,导体对电场的分布能够起到调整和控制作用.在生产实践和科学实验中,常常需要一定场强分布的电场,试图通过电荷分布来产生这种电场是很困难的,因为电荷分布不易调整和控制.通常的办法是制作一些一定几何形状的导体,并按一定的相对位置放置,然后给它们加上适当的电势,来产生所需要的电场.由于导体的配置和其上的电势可以人为地安排和控制,这样就可以得到我们所需要的各种电场. 如图2.2所示,一个导体(píng)面电极K(电势为120V),在它前面放置一个中央带有圆孔的导体(píng)面电极G(电势为30V)的导体带电系统.这个带电系统产生的电场分布情况在图2.2中用等势面分布表示了出来.在圆孔处,等势面向右侧凸起,从而使电场线在孔附近不再是(píng)行线,而是具有垂直于中心线(轴)向外辐射的场强分量E,,设想从K电极中心发射出一束电子,当它们经过圆孔后,电场的E,分量就使电子受到向交轴集中的电场力,结果会使电子束在点F会聚起来.这个带孔导体板对电子束的作用,就好像凸透镜对光束的作用一样,可以达到聚焦的目的.这种方法叫静电聚焦,带孔导体板G叫做静电透镜.在示波器、电视机显像管中,为使电子束会聚在荧光屏上形成清晰的光点,都需要这种电子束聚焦装置.
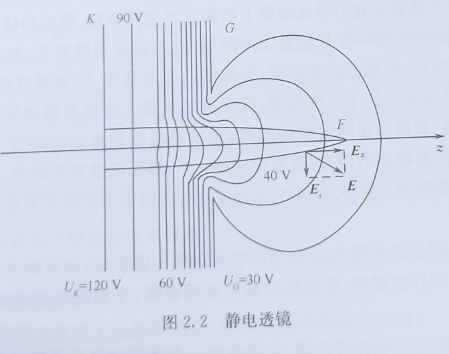
图2.2 静电透镜体内 |