电工基础:RC电路的零输入响应(41)
|
电感元件和电容元件在电路中是非常常见的,它们在电路中的接法不同,以致它们发挥的作用不同。电容元件经常作为过电压保护元件并联在电路中,它主要利用电容元件在换路瞬间电压不能发生跃变这一原理进行工作的,这其实是一个电容的放电过程。
上一次技成培训网给大家分享的是动态电路的初始值的计算,这一次我们继续学习它的过渡过程。分析动态电路的过渡过程的方法之一是:根据KCL、KVL和支路的VCR建立描述电路的方程,一般是已知激励(电源电压或电流),然后求解微分方程,从而得到电路的响应(电压或电流)。这种方法称为经典法。由于电路的激励和响应都是时间的函数,所以这种分析也是时域分析。
我们先来学习RC电路的零输入响应。所谓零输入响应,是指动态电路中无外施激励电源,输入信号为零,仅由动态元件(电感元件或电容元件)的初始储能所产生的响应。下图41-1所示的RC电路中,换路前,电容C已充电,其电压uC=U。
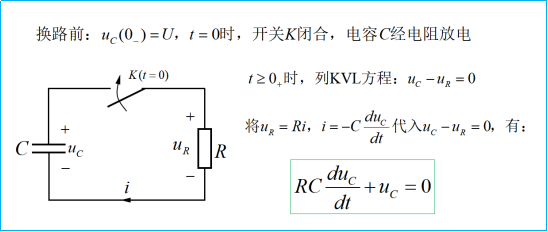
图41-1
图41-1中的电流、电容电压与电阻电压都是用小写,这是表示它们是瞬时值。而i=-CduC/dt中的负号,是因为电容电压和电流是非关联参考方向,这也表明电容是放电的。根据KVL和VCR建立方程,可以得到一个一阶齐次微分方程。所谓一阶,是指方程中关于uC的导数是一阶导数(duC/dt),在电路中表现为仅含一个储能元件或可等效为一个储能元件的电路;齐次在这里指的是等号右边为零。关于微分方程,大家也不必深究,知道是什么就行,我们要知道的是这个方程是怎样建立起来的。
图41-1中关于RC动态电路的零输入响应所建立的一阶齐次微分方程,其初始条件uC(0 )=uC(0-)=U,即换路前后(开关闭合)瞬间电容电压uC不能突变,为电容初始电压U。微分方程的计算过程我们不用管,直接引用它的通解公式,即令方程的通解uC =Aept,如图41-2所示。将该通解代入图41-1的方程中,得到其特征方程,特征根为p=-1/RC。然后根据uC(0 )=uC(0-)=U,令t=0,代入通解公式uC=Aept中可以得到积分常数A=uC(0 )=U。这样,求得满足初始值的微分方程的解如图41-2所示。式(3)就是电容元件放电过程中的电压uC的表达式。

图41-2
根据电容元件放电过程中的电压uC的表达式和KVL、VCR,可以得出,电容的电流与电阻的电压如图41-3所示。

图41-3
从这些表达式可以看出,电压uC、uR以及电流i都是按同样的指数规律从初始值衰减的,它们衰减的快慢由1/RC决定。根据方程的特征根p=-1/RC,仅取决于电路的结构和元件的参数。引入时间常数τ,令τ=RC,称为RC电路的时间常数。可以称τ为时间常数,这也是因为,当电阻的单位为Ω(R=u/i,即伏/安),电容的电位为F(C=idt/du,即安·秒/伏)时,乘积RC的单位为秒(s)。

图41-4
引入时间常数τ后,电容电压uC和电流i的表达如图41-4。τ的大小反映了一阶电路过渡过程的进展速度,它是反映过渡过程特征的一个重要的量。可以计算得时间t分别等于0和τ时的电容电压值。即经过一个时间常数τ后,电容电压uC衰减了63.2%。或者说,
时间τ表示了电压uC衰减到初始值U的36.8%所需的时间。分别计算出t=τ,t=2τ,t=3τ,…时刻的电容电压值列表如图41-5所示。从表可见,理论上认为经过无限长时间(t=∞)uC才能衰减为零值。但工程上一般认为换路后,经过3τ~5τ时间过渡过程即告结束。也就是说,经过3τ~5τ时间后,电容放电基本结束。
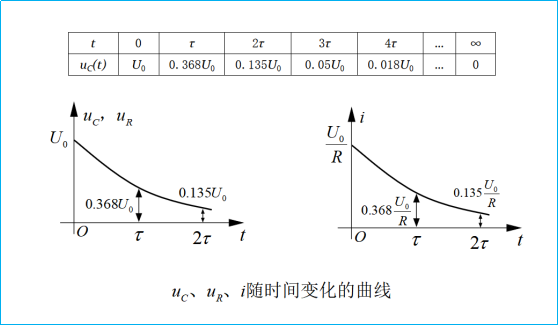
图41-5
RC动态电路的电压uC、uR及电流i随时间变化的曲线如图41-5所示。在放电过程中,电容不断放出能量并被电阻所消耗;后,原来储存在电容中的电场能量全部为电阻吸收而转换成热能。(技成培训原创,作者:杨思慧,未经授权不得转载,违者必究!)
相关课程: 电工基础 |