傻傻分不清电路?专业电气学姐为你全方面解读(十五)
|
对于《电工基础》,如果能持续学习的,我想到目前为止也必定是累积了不少的知识,特别是电路分析的相关知识,例如支路电流法、网孔电流法、节点电压法和叠加定理等,这些也是课程的难点所在,想要熟练掌握就离不开练习。
不管是什么方法,万变不离其宗,其实它们都是在遵循基尔霍夫定律的基础上演变推理得来的。甚至你们有自己的一套电路分析方法,也不妨让大家相互学习一下。
我们上次学习的是叠加原理、即叠加定理的相关知识,简而言之就是对电路中的各个独立电源进行分开处理,然后再对各个分电路进行电压、电流的叠加。而这次我们接着学习的是戴维南定理,说白了就是电路的等效变换。
提到电路的等效变换,大家会不会联想起什么呢?其实我们在之前就已经学过电路变换的相关知识,那就是电压源与电流源的等效变换及星形-三角形连接电阻的等效变换,显然,现在又多了一个戴维南定理。那么,我们开始进入这次的学习分享吧。
在学习戴维南定理之前,我们先来学习一个新的概念:二端网络。
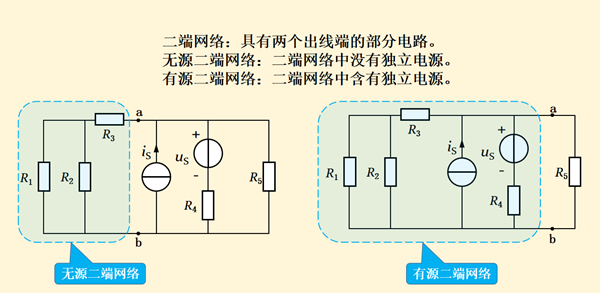
图15-1
二端网络就是具有两个出线端的部分电路,如图15-1所示的闭合面部分,a、b为两个出线端,即a-b端口,包括无源二端网络和有源二端网络。在曹老师的课程内容中,无源二端网络是二端网络中没有电源;有源二端网络是二端网络中含有电源。
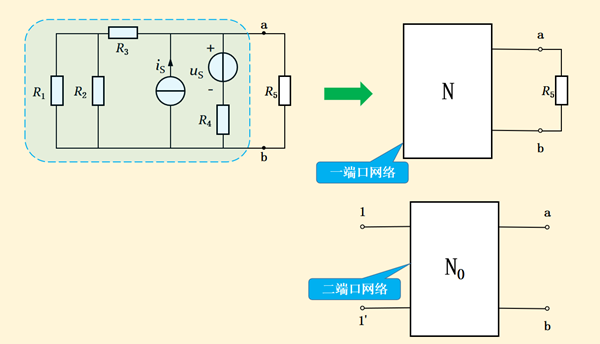
在这里我要对曹老师的课程内容进行补充说明一下,所谓电源其实指的是独立电源,独立电源是区别于下次要学的受控电源。理想情况下,独立电源两端的电压或电流是恒定的,如干电池、发电机等;而受控源两端的电压或电流是可变的,如模拟电路中的放大电路等。另外,二端网络也叫一端口网络,所以无源二端网络也可以称为无源一端口网络,有源二端网络也可以称为含源一端口网络。如下图15-2所示,一端口网络只有一个端口a-b,以供与外电路连接,而二端口网络有两个端口1-1’和a-b,四个接线端。
图15-2
对于无源二端网络(仅含线性电阻),根据线性电路的性质,我们可以通过利用电阻的串并联和星形-三角形连接的等效变换简化为一个电阻,即等效电阻。对于一个既含线性电阻又含独立电源的有源二端网络,又该如何化简呢?或者说它的等效电路是什么?戴维南定理和诺顿定理可以回答这个问题。
戴维南定理,又称戴维宁定理,它表示:任何一个有源二端线性网络,都可以用一个理想电压源和电阻串联的组合来等效代替。 诺顿定理:任何一个有源二端线性网络,都可以用一个理想电流源和电阻并联的组合来等效代替。
基于戴维南定理和诺顿定理在电路分析中的解决方法大同小异,曹老师仅对戴维南定理进行展开讲解,所以诺顿定理我也就不作详解,大家感兴趣的可以私下自行学习。
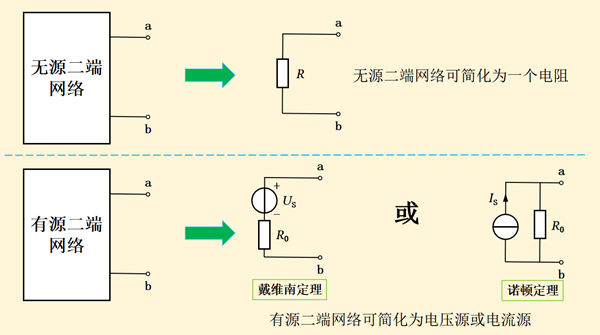
图15-3
图15-3示出无源二端网络和有源二端网络的化简。我们可以看到,有源二端网络和无源二端网络所化简的电路,区别也是在于是否含有电源。根据戴维南定理可以把有源二端网络化简为带内阻的电压源,诺顿定理可以把有源二端网络化简为带内阻的电流源。我们以一个例子来推理一下有源二端网络的等效替换过程,如下图15-4所示。
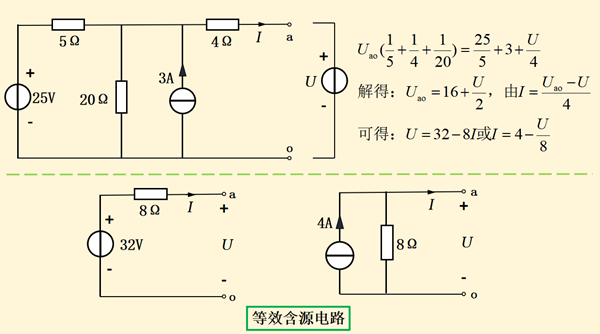
图15-4
从等效的简化电路与原来的一端口必须具有相同的端口外特性出发,图15-4中原电路是一个含源一端口,为了求其端口的伏安特性,可以设想在端口a-o处加一个电压源U,然后求解端口电流I,从而得出U和I的函数关系。利用节点电压法列出节点电压方程求解,如图15-4所示,化简出来的结果用含源支路表示,左边的称为戴维南等效电路,右边的称为诺顿等效电路。
这里的“等效”是指对端口外等效,其内部不等效。例如图15-4中的原电路和戴维南等效电路对比,原电路内部的部分电阻中是有电流流过的,即内部电路有功率的消耗,而戴维南等效电路显然不存在功率的消耗。
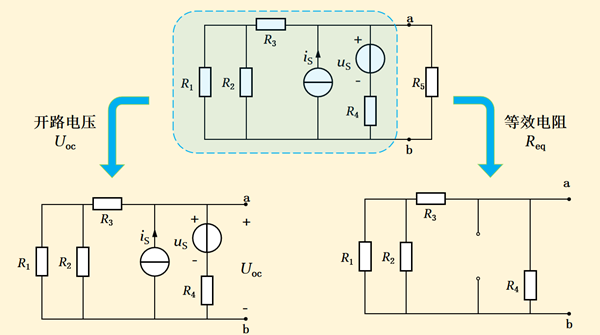
根据戴维南定理,其等效电路中,电压源的电压等于有源二端网络的开端电压,即出线端开路时网络在端口上的电压;等效电压源的内阻等于有源二端网络相应无源二端网络的输入电阻,即把网络内部全部电源置零后的输入电阻。图15-5示出了其变换电路的处理。
图15-5
在图15-5中,我们可以看到,在计算开路电压时,把端口外电路部分去掉,即端口作开路处理;在计算等效电阻(内阻)时,把所有独立电源置零,即把电压源作短路处理,把电流源作开路处理。
在使用戴维南定理进行电路分析计算时,有3个步骤:
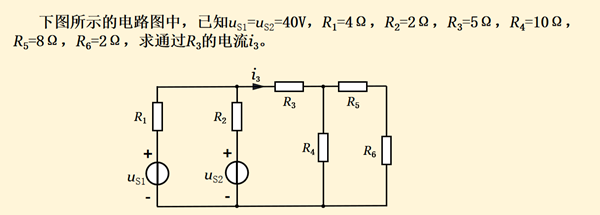
(1)求出有源二端网络的开路电压uoc; (2)将有源二端网络的所有独立电源置零,即将电压源短路,电流源开路,求出无源二端网络的等效电阻Req。 (3)画出戴维南等效电路图。 接下来我们以一个例题来理解戴维南定理的应用,如下图15-6所示的例题。
图15-6
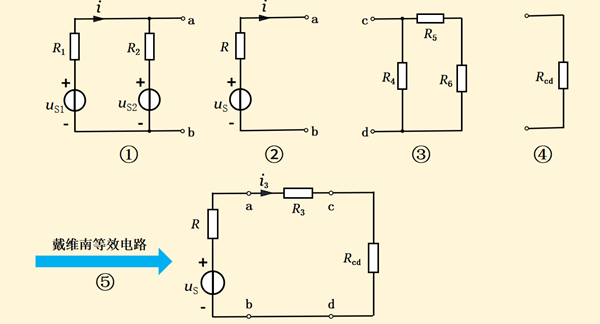
我们将电阻R3的左右两部分的电路都看为二端口网络从而加以简化。左侧是一个含源一端口,求开路电压及等效电阻较为方便,它的等效电路图如下图15-7的②所示;再求右侧的无源一端口的等效电阻,如图15-7的④所示;后画出简化电路图,进而求出通过R3的电流i3。
图15-7
图15-7中的①图简化为②图、③图简化为④图的计算过程与结果如图15-8所示;后计算出通过R3的电流i3。
图15-8
通过例题我们可以看到,戴维南定理的应用在电路分析中是非常方便的,大大减少了解题的步骤,而且条理清晰,不容易弄混,希望大家都能掌握这部分内容。 至此,戴维南定理的讲解就结束啦!曹老师在课程中还讲解了好几道例题,大家如果想熟练掌握戴维南定理的知识,还是很有必要去听一下的。那么,后已几道题结束本次的学习分享吧。(技成培训原创,作者:杨思慧,未经授权不得转载,违者必究!)
相关课程推荐:
电工基础
|