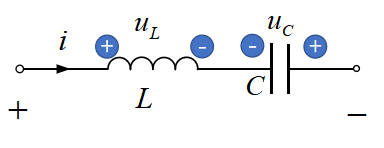交流电路中的电感与电容

电感与电容作为储能元件和动态元件，在工程技术中的应用非常广泛，如在电子电路中的滤波、谐振，在电力系统中的补偿、功率传输等。（更多电工课程免费试看）

当然，实际上的电感线圈和电容器多多少少都会有损耗，即存在电阻，例如电动机线圈的电阻有几欧到几十欧不等，电容的电阻相对较小。

总的来说，电感和电容在直流电路中的应用相对较少，例如电感线圈可以用于电磁铁的励磁，电容器可以用于隔直或储能。它们更多的是应用于交流电路。

那么，电感和电容在交流电路中又有着怎样的表现呢？答案就让我来给大家揭晓吧！

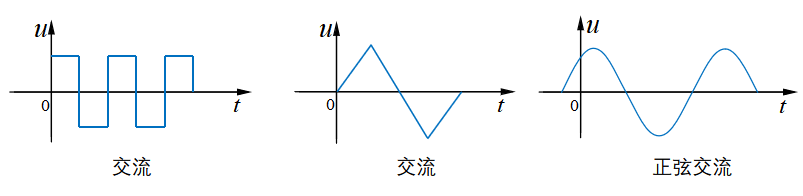
一、正弦交流电路

所谓交流电路，是指电路中的电压和电流随时间作周期性变化的电路，如下图1-2所示。而上文所提及的交流电路，都是指的正弦交流电路。正弦交流电路的电压和电流随时间做正弦规律变化。这里的“正弦规律”可以是正弦函数，也可以是余弦函数，这是因为正弦函数和余弦函数的变化规律相同，它们两者间的区别仅在于相角差。另外，正弦交流电路也是我们日常生活工作中所接触的电路。

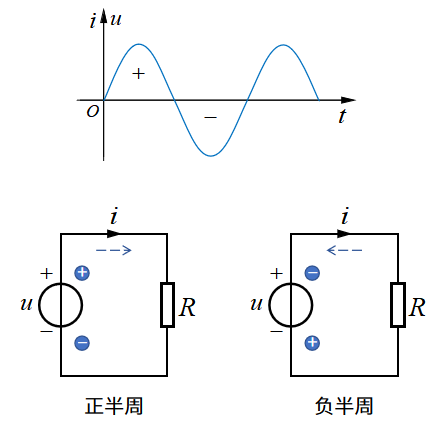
显然，正弦交流电路中电压、电流的大小和方向都随时间变化，而在电路中，往往需要标定两者的方向，所以这里就涉及到了参考方向和实际方向的问题。如图1-3所示，假定交流电压源的电压参考方向为上正下负，电流的参考方向为从左到右。

结合电压电流波形，当电压、电流波形为正半周时，表明其实际方向和参考方向一致；当波形处于负半周时，表明电压和电流实际方向和参考方向相反，图1-3中的蓝色图形为实际方向，黑色为参考方向。

大概了解正弦交流电路后，我们进入这次分享的主要内容。

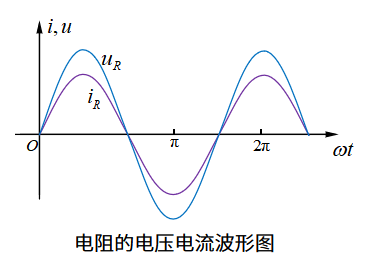
二、交流电路中的电感和电容

对于电阻而言，流过电阻的电流与电阻两端的电压同步变化，所以不管是大小还是方向，都保持一致的趋势，如图1-4所示。换言之，其电压和电流之间之间的区别仅在于一个比例系数，这个比例系数就是电阻值。

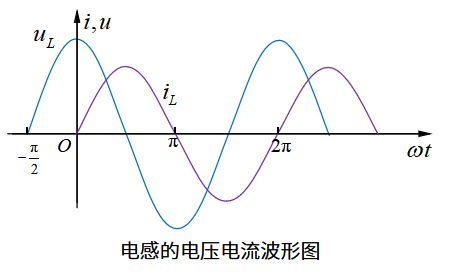
但电感和电容比较特别，它们两者的电压和电流都不是同步变化的，而是有一个相位差。所谓相位差，可以理解为电压和电流的变化趋势差，例如在电感元件中，当电流在计时零点的值为零，且随时间变大时，电压在计时零点的值却为最大值，且随时间变小，如下图1-5所示。

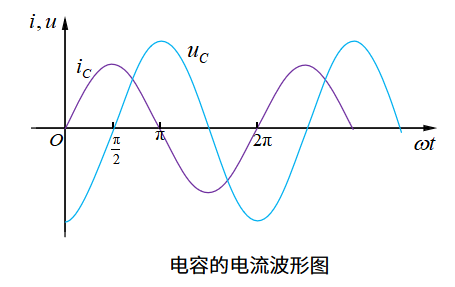
图1-5所示的电感电压电流波形图，表示了电感的电压超前电流90°，因为撇开时间，仅从波形图来看，两个波形的零点（都是正斜率或负斜率）间最小角度为90°。为什么电感的电压和电流不同步呢？这是因为电感的电压和电流不是正比例关系，而是成微分关系，所以不像电阻那样简单。

类似的，电容的电压和电流也有一个相位差。但区别于电感，在电容元件中，当电流在计时零点的值为零，且随时间变大时，电压在计时零点的值却为最小值（负值），且随时间变大，如下图1-6所示。

电容的电压与电流存在相位差的原因与电感一样，都是因为其电压和电流不是正比例关系，但电容的电压与电流成积分关系，所以电感和电容两种的电压电流关系也有区别。为了让大家能够直观看出这个区别，我们以电感和电容的串并联电路为例。

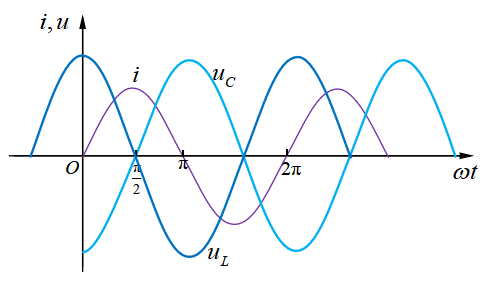
1、电感和电容串联时的电压电流关系

如图1-7所示，电感和电容串联，所以它们流过同一个电流。但它们不会因为串联而导致各自电压电流关系变化，所以依然是如图1-5和图1-6所示的关系。显然，基于同一电流的情况下，电感的电压和电容的电压处于反相关系。

简单来说，就是在LC串联的正弦交流电路中，任一时刻，电感电压和电容电压方向相反，如图1-8所示。另外，大家可以举一反三，思考一下，是否存在电感电压与电容电压方向相反、大小相等的情况呢？

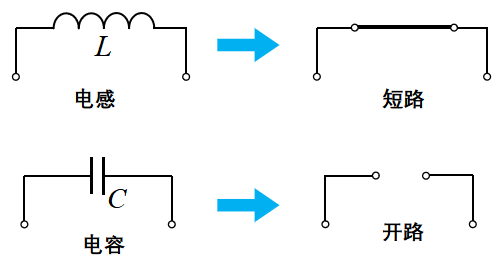
显然是存在的，且当电感电压和电容电压大小相等、方向相反时，电感电容的串联组合对外就相当于短路，因为其组合两端的电位相等，大家可以自行赋值举例进行理解。就好比拿两个电压相等的干电池以正极接正极的方式串联，对外没有电压。LC串联电压反相，那并联会怎样呢？我们接着往下看。

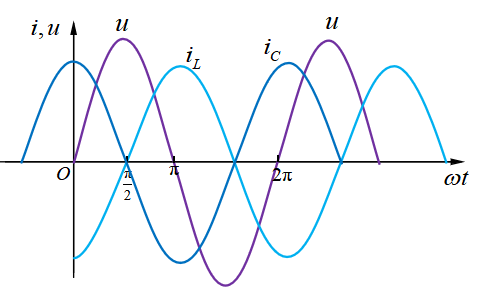
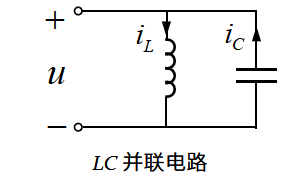
2、电感和电容并联时的电压电流关系

电感和电容并联，所以它们承受同一个电压。同样的，它们并不会因为并联而导致各自电压电流关系变化，所以依然是如图1-5和图1-6所示的关系。显然，基于同一电压的情况下，电感的电流和电容的电流处于反相关系，如图1-8所示。

简单来说，就是在LC并联的正弦交流电路中，任一时刻，电感电流和电容电流方向相反，如图1-10所示。另外，大家仍然可以举一反三，思考一下，是否存在电感电流与电容电流方向相反、大小相等的情况呢？

显然也是存在的，且当电感电流和电容电流大小相等、方向相反时，电感电容的并联组合对外就相当于开路，因为它们的电流和为零，对外没有电流。为了便于理解，大家可以自行赋值举例，在此我就不再过多阐述。就好比拿两个电压相等的干电池以首尾相连的方式并联，对外没有电流。

综上所述，当电感和电容串联时，两者电流相等，电压反相，若电压大小相等，其串联组合就相当于短路，这也叫电感和电容的串联谐振；当电感和电容并联时，两者电压相等，电流反相，若电流大小相等，其并联组合就相当于开路，这也叫电感和电容的并联谐振。关于谐振的更多内容，基于其内容较为复杂，在此我也不再展开讲解。

至此，这次的分享就到这里，感谢大家的阅读。